Research

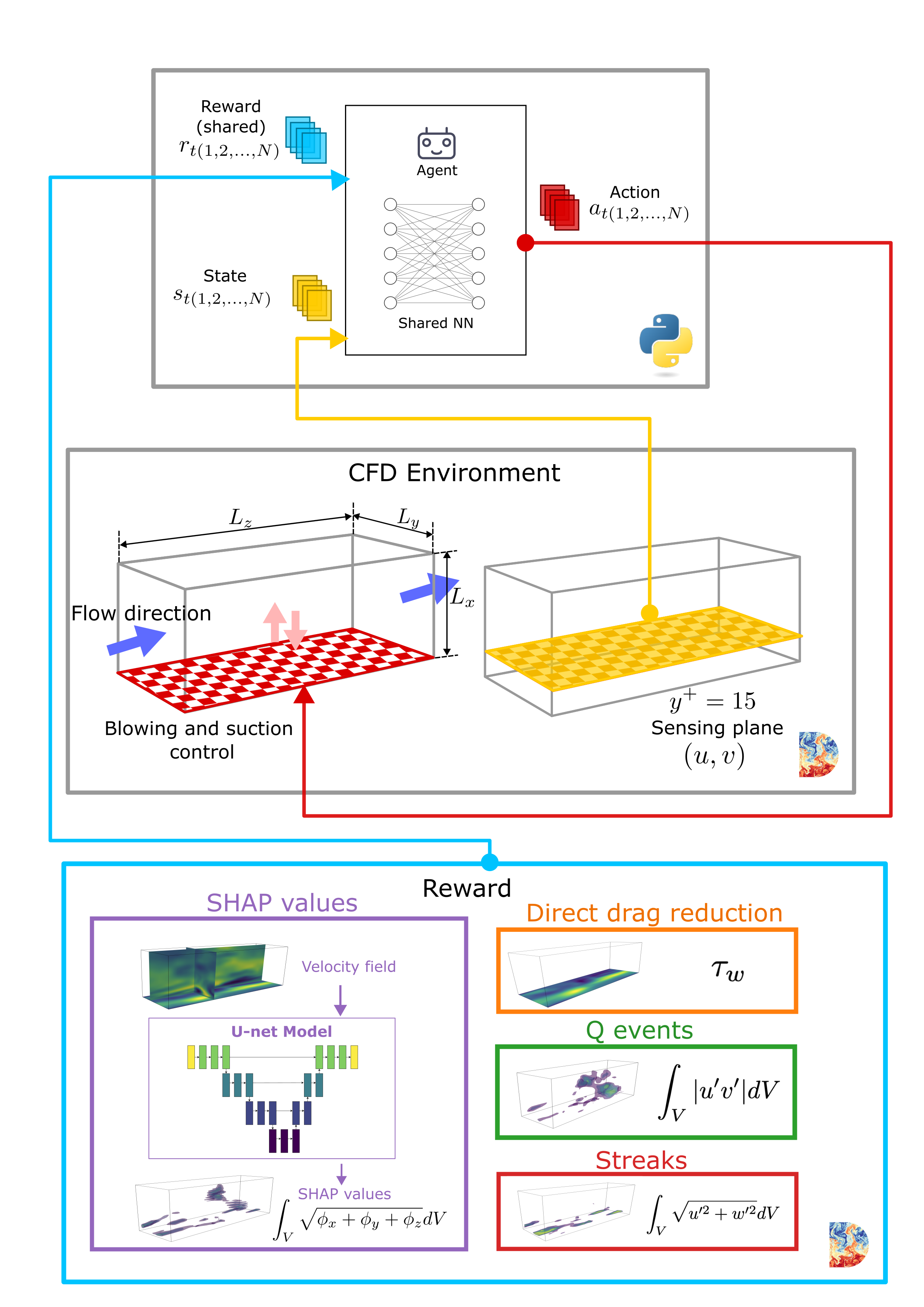
Data-driven methods, Nonlinear dynamics, and Transition

Ddata-driven methods have expanded the toolbox available to approach fluid problems. Deep reinforcement learning (DRL) has emerged as a particularly powerful approach to reveal new, more effective control strategies. We have used DRL to control turbulence in channel flow configurations, aiming to reduce physically relevant coherent structures in the flow.

We have also extensively used ideas from dynamical systems to study the transition to turbulence in Newtonian flows, in particular in boundary layers, which are greatly challenging due to the spatially-developing nature of the flow. Here, we identified a separatrix between laminar and turbulent states dubbed ’the edge of chaos’ as well as elements that exist within this co-dimension one manifold: ’the edge state’ (states with only one unstable directions pointing out of the edge manifold) and ‘minimal seeds’ (the most dangerous perturbations in terms of energy).

We use these ideas to better understand transition to turbulence, and to tame turbulent flows.

Viscoelastic Flows

MMany liquids in industry and biology are viscoelastic (like paints, blood, saliva, and DNA suspensions among many others), displaying a mixture of both viscous and elastic properties. These fluids are fundamental for a myriad of industrial processes (such as mixing of chemicals or cooling of microprocessors), however they are still not well understood due to the complexity of the mathematical models that describe them. The current consensus is that there are three “types” of viscoelastic chaos: modified Newtonian turbulence, elastic turbulence, and elasto-inertial turbulence.

We’ve identified a linear instability present in the arguably most popular viscoelastic model (FENE-P), and we have shown that this instability is capable of triggering chaotic dynamics with and without inertia. We’ve also studied the state-space of elasto-inertial turbulence, revealing that up to four different attractors (an arrowhead, a chaotic arrowhead, the laminar state, and elastoinertial turbulence) can be present for the same parameter regime.

We hope to better understand the origins of and the connections between the chaotic states in viscoelastic turbulence in this project.

Miscellaneous

In 2024 I took part in the workshop “Non-Newtonian Flows in Porous Media” at the Banff International Research Station. My talk about “Instabilities in rectilinear flows and their link to viscoelastic turbulence with and without inertia” is available here!

In 2020 During the Covid-19 crisis I tried to introduce Chaos and Nonlinear Dynamics for kids who could not go to school due to the lockdown in many countries in an online lesson together with Encounteredu. The video is available here!

I am also enthusiastic about science communication and reading about maths and physics in general. It is always great checking Quanta Magazine and FYFD among others. I am interested in open-source software and in the Julia programming language. A very flexible tool that I use in my research is the general purpose spectral solver Dedalus.